Who was Pythagoras?
If you hate maths then possibly the man to blame is Pythagoras of Samos. Before Pythagoras was a theorem he was a man who, aside from allegedly formulating this famous theorem coined the term philosopher, founded the Pythagorean Brotherhood, and discovered the fundamental relationship between musical notes that explained why some notes sound pleasant when played together and some don’t (regardless of musical taste!).

All the maths you learn at school is based on what is called ‘numerical logic‘ and, unfortunately, if you don’t get the logic then you won’t get very far with the maths. The purpose of making students learn Pythagoras’ Theorem was to introduce the idea of numerical logic. The problem today is that the purpose behind the teaching seems to have been lost and students find themselves having to learn the theorem for its own sake.
The real world is full of uncertainty. Not just the risk of war or famine, but also little uncertainties – like where did I leave my key? Did I switch the kettle on? Have I put the potatoes in the oven? What time is it? Our individual understanding of how the world works depends on how we observe it. This depends not only on how good our senses are but also on how we interpret what we observe. The whole process of understanding the world around us is extremely fragile. You might have some form of sense impairment; you might be drunk or hallucinating. It is all too easy to change the way we see the world. Because we are all different then we can all see the world in markedly different ways.
The genius of Pythagoras was that he understood that the world could be explained by numbers and that the way the numbers worked and interacted with one another happened regardless of individual observation and understanding. So, although it sounds a bit harsh if you don’t, Pythagoras’s Theorem works whether you understand it or not. You can still use the theorem just by plugging in the numbers and it still works. Numerical logic tells us all about the relationship between numbers. Do you understand that 1 + 1 = 2 ? Take 1 from 2 and you have 1 left over? If so, then read on…
What is Pythagoras’ Theorem?
Pythagoras discovered that if you drew any right-angled triangle then there is a fundamental relationship between the lengths of the three sides.
Basically he proved that if you measured each side, as I have done below…
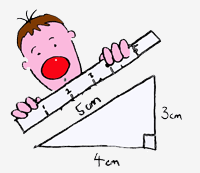
…then I calculate the square of each number…
\(5^2 = 25\)
\(3^2 = 9\)
\(4^2 = 16\)
…then if I add the squares of the shorter two lengths together then this adds up to the square of the longest length.
\(9 + 16 = 25\)
Have a go…
Try drawing yourself a few right-angled triangles (best to use a set square to give an accurate right angle) and calculating the square of each length and seeing if adding the squares of the shorter lengths gives you the square of the longest length.
Proving Things Mathematically
Perhaps this works for every right-angled triangle? Well maybe… and here is where science and maths take very different paths. Now I have a theory that maybe if you take the squares of the two shorter lengths and add them together you get the square of the longer length. The experimental physicist in me would say that now we have a model for the relationship between lengths in a right-angled triangle we can now predict the lengths in some different triangles and then we can perform some tests to see if our predictions are correct. Lets try it now.
Here is a triangle…
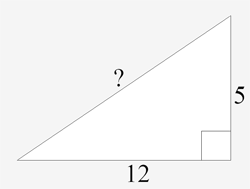
A right angled triangle with shorter sides 5 and 12. The length of the longest side is missing.
The right-angled triangle above has two shorter lengths of 5cm and 12cm. What is the longest length? The squares of these numbers are 5 x 5 = 25 and 12 x 12 = 144. So the square of the longest length will be 25 + 144 = 169. I plug that number into my calculator and find the square root which gives me 13. So I predict that the length of the longest side will be 13cm. Try drawing it and see what you get.
This is the basis of the scientific method and that’s fine but how can you be confident that this will work for all right-angled triangles? Well, following the scientific method you can’t – you are always left with doubt. What does the mathematician in me have to say? By following numerical logic you can create a proof that leaves you in no doubt as to the relationship between the three sides. Here goes…
Proving Pythagoras’ Theorem
Lets draw a square…

And inside another square…

You can see that now I have a large square and inside 4 small right-angled triangles and a smaller square. The lengths of the sides of these shapes could be any number so I’ll just identify them with letters…
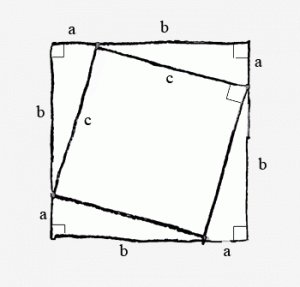
The length of one side of the large square is a + b. So we can see that the area of the large square is (a+b) x (a+b), or (a+b)2.
This can be multiplied out as follows…
\((a+b)(a+b) = a^2+b^2+2ab\)
So the area of the large square =
\(a^2+b^2+2ab\)
Or I can calculate the area of the large square by calculating the areas of the 4 right-angled triangles and the smaller square and adding them together…
The area of a triangle is ½(base x height), so the area of one little triange is
\(\frac{1}{2}(a \times b)\)
But we have 4 of them so that is
\(4 \times \frac{1}{2}(a \times b) = 2ab\)
Also we have the area of the smaller square
\(c \times c = c^2\)
So the area of the large square =
\(c^2 + 2ab\)
…so the area of the large square can be either
\(a^2+b^2+2ab\)
or
\(c^2 + 2ab\)
As they both represent the area of the large square we can make these two expressions equal one another…
\(c^2 + 2ab = a^2+b^2+2ab\)
If we cancel the 2ab that appears on both sides of the equals sign then we are left with
\(c^2 = a^2 + b^2\)
And there we have a mathematical proof showing the relationship between the sides of any right-angled triangle. We got there by using numerical logic, something quite different to using the scientific method. This relationship is one that you will have to learn and be expected to know and be able to use (it will not be given to you in an exam!).
Below is a link to our latest Maths Graffiti video showing you this proof in action!
Pythagoras’ Theorem is usually presented in modern textbooks and in school lessons as simply
\(c^2 = a^2 + b^2\)
The old-fashioned way of learning the theorem is probably more useful in helping you to understanding the relationships between the lengths of a right-angled triangle…
“For a right-angled triangle the square on the hypotenuse equals the sum of the squares on the other two sides”
This is more useful because it expresses in full English what
\(c^2 = a^2 + b^2\)
actually means. It is useful also because you will have to know what the hypotenuse is. The hypotenuse is the special name given to the longest length in a right-angled triangle. It is a Greek word which means ‘opposite to and extending from one side to the other of’, in this case opposite to and extending from one side to the other of the right angle.
National 5 students often ask me if it is important to understand numerical logic for the exam. The answer, I’m afraid, is “yes” as the following type of question often stumps students…
Q. Prove that triangle A and triangle B are congruent.
Pythagorean Triples
As this is a topic that teachers often miss in class it is a good idea for us to have a brief look at what are called Pythagorean triples. Basically a Pythagorean triple is three whole numbers that fit into Pythagoras’ equation. The basic triple is a 3,4,5 triangle, which we saw above. Another (which appears less frequently) is the 5, 12, 13 triangle – which we also looked at above.
Pythagorean triples quite frequently appear on non-calculator papers (and sometimes on calculator papers) just to see if you are on your toes. I have seen foundation level papers asking students to construct right-angled triangles whose lengths are basically Pythagorean triples (it makes the question easier to mark!).
