Have you checked out our first Maths Challenge on our Facebook page? During the current tutoring post-exam lull I’ve been picking up a few old interests of mine, one of which is creating an effective Sudoku solver app. And the first stage in solving a Sudoku puzzle is to understand the maths of magic squares.
So what’s mystical about a Magic Square?
Through almost all recorded history numbers have had a mystical quality about them. Pythagoras (of Pythagoras’ Theorem fame) built a religious cult based around numbers where every number was given a special meaning: for example, the Pythagoreans believed the number \(1\) represented man, \(3\) represented woman, \(5=2+3\) is marriage between a man plus a woman – and so on. This idea has carried on through to the present day with numerologists attempting to draw relationships between numbers and events. For instance, John F Kennedy was killed by Lee Harvey Oswald, born in 1939, and Abraham Lincoln was killed by John Wilkes Booth, born in 1839, giving the number 39 a special meaning in this context. Have you spotted that the names Lee Harvey Oswald and John Wilkes Booth contain 15 letters? No: neither did I. Some coincidence? Possibly… and the words ‘some coincidence’ also contain 15 letters so perhaps it’s more than a coincidence…
… Anyway, numbers which, as we can see, even by themselves might be considered mystical also have a prominent place in divine texts.
To understand what puts the magic in magic squares we need to believe that events can’t be random because all events must be the will of beneficent or vengeful deities. For the sake of the argument let’s refer to such deities or supernatural entities – Him/Her/Them – as ‘God’, which is how most of our ancestors (and indeed some of our peers) would have it. So, if we live in a universe created by God and driven by God’s will then we argue that if I throw a number of sticks and they land in a particular way then this isn’t chance: it is God’s will. If I throw pebbles in the air then how they fly and where they land is God’s will. When all is God’s will then nothing is left to chance and luck doesn’t exist. Now let’s say we can associate numbers with these seemly random events. Perhaps then we can use these numbers to be able to understand the will of God? Well, possibly… This concept of linking numbers with random events and then associating this with divine power is called Cleromancy, a concept argued over by most major religions in their time.
An obvious example of how numbers from seemingly random events can be used to divine the future is the I Ching – the Book of Changes. Six numbers between \(6\) and \(9\) are turned into ‘hexagrams’ (basically special symbols) which can then be looked up in the book and interpreted (how the present will change to become the future). And the I Ching does indeed contain a magic square:
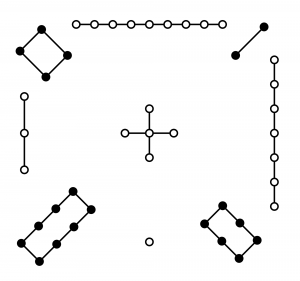
Count up the dots and see that any of the rows, columns and diagonals of this square add to 15. We’ll delve into the I Ching magic square later in this post.
The Judeo-Christian Bible certainly contains the idea that God’s will can be determined by seemingly random events (‘the casting of lots’). Magic squares started to appear in Christian manuscripts from the Medieval period onward. And we see a well known magic square carved into Barcelona Cathedral (a relatively modern building generally dripping with symbolism):

Any of the rows, columns and diagonals of this square add to 33, the age of Christ when he died.
One of the best magic squares to study appears in Albrecht Dürer’s Melencolia I engraving of 1514:

Let’s take a closer look at the magic square in this picture. You’ll see that each column, row and diagonal add to 34, and also each of the four squares in the corners add to 34, making it even more magical. And, not just that, the bottom two squares say 1514 which is when Dürer made the engraving.

Finally, here is a magic square I just made for myself while putting together this post. Each column, row and diagonal add to 45 (which I chose because that’s how old I am):

Magic Square Maths
Let’s look again at the 3×3 I Ching magic square. Here it is using numbers instead of dots:
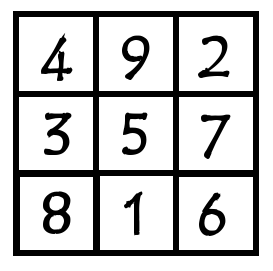
Let’s take a look at the sequence of numbers 1 to 9 used in the I Ching square. If we think about each row (likewise columns and diagonals) having to add together to make the same number, \(M\), then we have
\(1+2+3+4+5+6+7+8+9=3M\)
\(45=3M\)
So,
\(M=15\)
The letter \(M\) is called the magic constant.
Now let’s check out the various ways of adding the numbers 1 to 9 to total 15. We’ll need eight different arrangements of these nine numbers because there are three rows, three columns and two diagonals. This may seem complicated but we can start by thinking that if 5 is in the middle then \(1+5+9=15\) and, working our way in towards the middle of the list, \(2+5+8=15\) and so on. Eventually you should have:
\(1+5+9=15\)
\(2+5+8=15\)
\(3+5+7=15\)
\(3+4+8=15\)
\(4+5+6=15\)
\(2+6+7=15\)
\(1+6+8=15\)
\(2+4+9=15\)
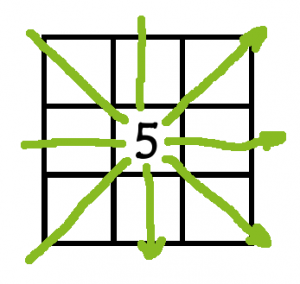
Now we have to decide what numbers go where. Again, this is more straightforward than it at first looks. The number in the middle needs to be included in four different arrangements (two diagonals, a column and a row). The number 5 is the only number to appear in four different arrangements so it must go in the middle:
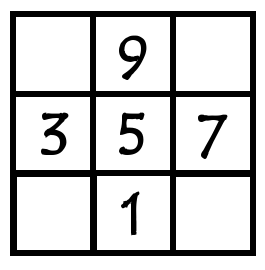
The numbers in the corners must appear in three different arrangements (a column, a row and a diagonal) so that means they have to be 2,4,6 and 8. That leaves the four numbers only appearing in two arrangements on the outer edges:
Completing the magic square is then simply a matter of filling in the gaps while ensuring that each row, column and diagonal adds to 15.
Have a go!
Try using the maths outlined in this post to generate your own 3×3 magic square based on a magic constant of your choice – perhaps your age or the day of the month on which your birthday falls (remember that the numbers can be positive as well as negative). Don’t just limit yourself to numbers. What about shapes? Or colours that mix together on the palette to make a single magic constant colour? If you come up with anything interesting then take a picture and post it below.
